• SSC Lunch Time Python
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

Lunch Time Python¶

Lunch 7: matplotlib¶

No description has been provided for this image

matplotlib is a plotting library for Python and the NumPy library. It is easy to use and can be used to generate scatter or bar plots, density maps and even 3D plots in publication quality.

Press Spacebar to go to the next slide (or ? to see all navigation shortcuts)

Lunch Time Python, Scientific Software Center, Heidelberg University

Advantages of matplotlib:¶

  • matplotlib is mostly used in conjunction with pyplot - a matplotlib module - that provides an easy-to-use interface
  • Very versatile, works with many types of data
  • Directly plot NumPy functions and arrays
  • Many export options
  • Customizable
  • Can be used with additional toolkits that extend the functionality, like seaborn

matplotlib installation¶

Available via pip:
python -m pip install -U matplotlib
Or install via conda:
conda install matplotlib

Basic plots¶

Plot the sin and cos over a range of angles. For this, we also need numpy.

In [1]:
import numpy as np
import matplotlib.pyplot as plt
In [2]:
xvals = np.arange(0, 2 * np.pi, 0.1)
In [3]:
plt.plot(xvals, np.sin(xvals))
plt.plot(xvals, np.cos(xvals))
Out[3]:
[<matplotlib.lines.Line2D at 0x7fd3e4558990>]
No description has been provided for this image

The default settions already look quite nice!

Running inside a script¶

Or more generally, if you want to suppress the output (return) of the plt() function.

In [4]:
plt.plot(xvals, np.sin(xvals))
plt.plot(xvals, np.cos(xvals))
plt.show()
No description has been provided for this image

plt.show() closes the plot; if you plot using a script and not a notebook, place one plt.show() command at the end of your script.

Running inside a notebook: static images¶

You can plot static images inside your notebook using the %matplotlib inline magic: You only need to run this once. It is not always necessary to put this, but it makes it clear which Matplotlib backend should be used.

In [5]:
%matplotlib inline
In [6]:
plt.plot(xvals, np.sin(xvals))
plt.plot(xvals, np.cos(xvals))
plt.show()
No description has been provided for this image

Scatter plot¶

In [7]:
xvals = np.random.randint(10, size=10)
yvals = np.random.randint(10, size=10)
plt.scatter(xvals, yvals)
plt.show()
No description has been provided for this image

Bar plot¶

In [8]:
xvals = np.linspace(1, 10, 10)
yvals = np.random.randint(10, size=10)
plt.bar(xvals, yvals)
plt.show()
No description has been provided for this image

Customizing plots¶

In [9]:
plt.bar(xvals, yvals, label="Random series")
plt.legend()
plt.show()
No description has been provided for this image

Customizing plots¶

In [10]:
plt.bar(xvals, yvals, label="Random series")
plt.legend(fontsize=16, loc="upper right")
plt.xlabel("Integer", fontsize=18)
plt.ylabel("Magnitude", fontsize=22, color="red")
plt.title("My custom plot", fontsize=22)
plt.show()
No description has been provided for this image

Customizing plots¶

In [11]:
xvals = np.arange(0, 2 * np.pi, 0.1)
plt.plot(xvals, np.sin(xvals), marker="x", markevery=10, color="blue")
plt.plot(xvals, np.cos(xvals), marker="<", color="black", alpha=0.5)
plt.show()
No description has been provided for this image

You can set x- and y-limits, annotate points on the plot, change the axis position and intersection, add a grid in the background, ...
A list of available markers is found here and named colors here.

Figure class: Advanced plots with the artist layer¶

A Figure in matplotlib is the whole plot (or window in the user interface) and can contain multiple plots. By accessing the Artist layer ("object-based plotting"), you can access more customizing options than with the basic plt.xxx Scripting layer ("procedural plotting") (see https://matplotlib.org/1.5.1/faq/usage_faq.html#parts-of-a-figure).

This also allows you to include multiple plots in one Figure.

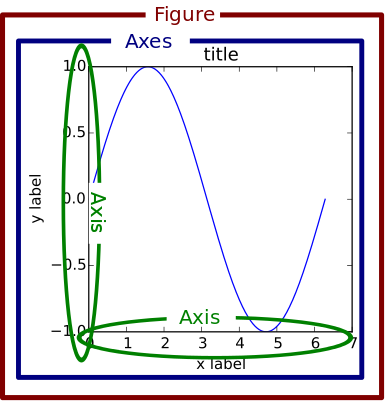
No description has been provided for this image
In [12]:
fig = plt.figure(figsize=(12, 10))  # width = 12 inches and height = 10 inches
# create one axes object
ax1 = fig.add_subplot(211)  # (2, 1, 1) no of rows, no of columns, no of plots
ax1.plot(xvals, np.sin(xvals), marker="x", color="blue")
plt.show()
No description has been provided for this image

It is also possible to use add_axes() instead of add_subplot(), but not recommended as with the latter, matplotlib takes care of the exact position of the axes in the figure.

Several subplots¶

Using add_subplot(), we can add one axes object at a time:

In [13]:
fig = plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(221)
ax1.plot(xvals, np.sin(xvals), marker="x", color="blue")
ax2 = fig.add_subplot(222)
ax2.plot(xvals, np.cos(xvals), marker="x", color="blue")
ax3 = fig.add_subplot(223)
ax3.plot(xvals, np.tan(xvals), marker="x", color="blue")
ax4 = fig.add_subplot(224)
ax4.plot(xvals, np.tanh(xvals), marker="x", color="blue")
plt.show()
No description has been provided for this image

A more practical way to add multiple subplots¶

In [14]:
fig, ax = plt.subplots(figsize=(12, 10), nrows=2, ncols=2)
ax[0, 0].plot(xvals, np.sin(xvals), marker="x", color="blue")
ax[0, 1].plot(xvals, np.cos(xvals), marker="x", color="blue")
ax[1, 0].plot(xvals, np.tan(xvals), marker="x", color="blue")
ax[1, 1].plot(xvals, np.tanh(xvals), marker="x", color="blue")
plt.savefig("my_figure.pdf", bbox_inches="tight")
plt.savefig("my_figure.jpg", dpi=300, bbox_inches="tight")
plt.show()
No description has been provided for this image

2D plots¶

In [15]:
def myfunc(x, y):
    return np.sin(np.sqrt(5) + x) * y


mf = 16
# the x and y values need to be spanned on a 2D mesh
num1 = np.arange(-5, 5, 0.1)
num2 = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(num1, num2)
In [16]:
print(X[0])
print(Y[0])

[-5.00000000e+00 -4.90000000e+00 -4.80000000e+00 -4.70000000e+00
 -4.60000000e+00 -4.50000000e+00 -4.40000000e+00 -4.30000000e+00
 -4.20000000e+00 -4.10000000e+00 -4.00000000e+00 -3.90000000e+00
 -3.80000000e+00 -3.70000000e+00 -3.60000000e+00 -3.50000000e+00
 -3.40000000e+00 -3.30000000e+00 -3.20000000e+00 -3.10000000e+00
 -3.00000000e+00 -2.90000000e+00 -2.80000000e+00 -2.70000000e+00
 -2.60000000e+00 -2.50000000e+00 -2.40000000e+00 -2.30000000e+00
 -2.20000000e+00 -2.10000000e+00 -2.00000000e+00 -1.90000000e+00
 -1.80000000e+00 -1.70000000e+00 -1.60000000e+00 -1.50000000e+00
 -1.40000000e+00 -1.30000000e+00 -1.20000000e+00 -1.10000000e+00
 -1.00000000e+00 -9.00000000e-01 -8.00000000e-01 -7.00000000e-01
 -6.00000000e-01 -5.00000000e-01 -4.00000000e-01 -3.00000000e-01
 -2.00000000e-01 -1.00000000e-01 -1.77635684e-14  1.00000000e-01
  2.00000000e-01  3.00000000e-01  4.00000000e-01  5.00000000e-01
  6.00000000e-01  7.00000000e-01  8.00000000e-01  9.00000000e-01
  1.00000000e+00  1.10000000e+00  1.20000000e+00  1.30000000e+00
  1.40000000e+00  1.50000000e+00  1.60000000e+00  1.70000000e+00
  1.80000000e+00  1.90000000e+00  2.00000000e+00  2.10000000e+00
  2.20000000e+00  2.30000000e+00  2.40000000e+00  2.50000000e+00
  2.60000000e+00  2.70000000e+00  2.80000000e+00  2.90000000e+00
  3.00000000e+00  3.10000000e+00  3.20000000e+00  3.30000000e+00
  3.40000000e+00  3.50000000e+00  3.60000000e+00  3.70000000e+00
  3.80000000e+00  3.90000000e+00  4.00000000e+00  4.10000000e+00
  4.20000000e+00  4.30000000e+00  4.40000000e+00  4.50000000e+00
  4.60000000e+00  4.70000000e+00  4.80000000e+00  4.90000000e+00]
[-5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.
 -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.
 -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.
 -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.
 -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.
 -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.]
In [17]:
fig, ax = plt.subplots(figsize=(15, 5), nrows=1, ncols=3)
ax[0].pcolor(X, Y, myfunc(X, Y), cmap="viridis")
ax[0].set_title("pcolor", fontsize=mf)
plt.show()
No description has been provided for this image

pcolor is the slowest plotting method of the three, but is more flexible in terms of the data mesh.

In [18]:
fig, ax = plt.subplots(figsize=(15, 5), nrows=1, ncols=3)

ax[0].pcolor(X, Y, myfunc(X, Y), cmap="viridis")
ax[0].set_title("pcolor", fontsize=mf)

ax[1].pcolormesh(X, Y, myfunc(X, Y), cmap="viridis")
ax[1].set_title("pcolormesh", fontsize=mf)

plt.show()
No description has been provided for this image

pcolormesh is basically identical to pcolor but faster.

In [19]:
fig, ax = plt.subplots(figsize=(15, 5), nrows=1, ncols=3)

ax[0].pcolor(X, Y, myfunc(X, Y), cmap="viridis")
ax[0].set_title("pcolor", fontsize=mf)

ax[1].pcolormesh(X, Y, myfunc(X, Y), cmap="viridis")
ax[1].set_title("pcolormesh", fontsize=mf)

ax[2].imshow(myfunc(X, Y))
ax[2].set_title("imshow", fontsize=mf)

plt.show()
No description has been provided for this image

imshow is the fastest of the three methods. Note that the image is flipped compared to pcolor and pcolormesh and that the axis range is specified differently.

In [20]:
fig, ax = plt.subplots(figsize=(15, 5), nrows=1, ncols=3)

ax[0].pcolor(X, Y, myfunc(X, Y), cmap="viridis")
ax[0].set_title("pcolor", fontsize=mf)

ax[1].pcolormesh(X, Y, myfunc(X, Y), cmap="viridis")
ax[1].set_title("pcolormesh", fontsize=mf)

ax[2].imshow(myfunc(X, Y), extent=[-5, 5, -5, 5], origin="lower", aspect="auto")
ax[2].set_title("imshow", fontsize=mf)

plt.show()
No description has been provided for this image

Here, we have repositioned the origin of imshow to match pcolor and pcolormesh, and further adjusted the aspect ratio and tick labels.

Imshow with contour bar¶

In [21]:
fig, ax = plt.subplots(figsize=(5, 5))

c = ax.imshow(myfunc(X, Y), extent=[-5, 5, -5, 5], origin="lower", aspect="auto")
cbar = plt.colorbar(c)
cbar.set_ticks([-5, -2.5, 0, 2.5, 5])
cbar.set_label("my colors", rotation=90, fontsize=mf)

ax.set_title("imshow", fontsize=mf)
plt.tight_layout()
plt.show()
No description has been provided for this image

3D plots¶

For 3D plots, you will need to import the mplot3d module. Then, when the axes are created, passing the projection="3d" keyword enables a 3D axes.

In [22]:
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
In [23]:
fig = plt.figure(figsize=(12, 12))
# fig, ax = plt.subplots(figsize=(12,12),subplot_kw=dict(projection='3d'))

ax = fig.add_subplot(projection="3d")
ax.plot_surface(X, Y, myfunc(X, Y), cmap=cm.viridis)


ax.set_title("3D plot", fontsize=mf)
plt.show()
No description has been provided for this image

The 3D plots of matplotlib are quite powerful but has its limitations: If it comes to plotting more than one set of data (two functions in one figure), then it will likely be rendered incorrectly.

In [24]:
fig = plt.figure(figsize=(12, 12))

ax = fig.add_subplot(projection="3d")
ax.plot_surface(X, Y, X + Y)
ax.plot_surface(X, Y, X + 0.1 * Y)


ax.set_title("3D plot", fontsize=mf)
plt.show()
No description has been provided for this image

For more advanced 3D plots, resort to Mayavi.

Interactive plots¶

In [25]:
%matplotlib notebook
In [26]:
fig, ax = plt.subplots(nrows=2, ncols=2)
ax[0, 0].plot(xvals, np.sin(xvals), marker="x", color="blue")
ax[0, 1].plot(xvals, np.cos(xvals), marker="x", color="blue")
ax[1, 0].plot(xvals, np.tan(xvals), marker="x", color="blue")
ax[1, 1].plot(xvals, np.tanh(xvals), marker="x", color="blue")
plt.show()

Further references¶

  • Anatomy of matplotlib: https://nbviewer.org/github/matplotlib/AnatomyOfMatplotlib/tree/master/
  • Matplotlib tutorial by Nicolas Rougier: https://github.com/rougier/matplotlib-tutorial
  • Creating animations with Matplotlib: https://matplotlib.org/stable/api/animation_api.html